Negative number
A negative number is any real number that is less than zero. Such numbers are often used to represent the amount of a loss or absence. For example, a debt that is owed may be thought of as a negative asset, or a decrease in some quantity may be thought of as a negative increase. Negative numbers are also used to describe values on a scale that goes below zero, such as the Celsius and Fahrenheit scales for temperature.
Negative numbers are usually written with a minus sign in front. For example, −3 represents a negative quantity with a magnitude of three, and is pronounced “minus three”. Conversely, a number that is greater than zero is called positive; zero is usually thought of as neither positive nor negative.[1] The positivity of a number may be emphasized by placing a plus sign before it, e.g. +3. In general, the negativity or positivity of a number is referred to as its sign.
In mathematics, every real number other than zero is either positive or negative. The positive whole numbers are referred to as natural numbers, while the positive and negative whole numbers (together with zero) are referred to as integers.
In bookkeeping, amounts owed are often represented by red numbers, or a number in parentheses, as an alternative notation to represent negative numbers.
Negative numbers appeared for the first time in history in the Nine Chapters on the Mathematical Art , which in its present form dates from the period of the Chinese Han Dynasty (202 BC. – AD 220), but may well contain much older material.[2] Indian mathematicians developed consistent and correct rules on the use of negative numbers, which later spread to the Middle East, and then into Europe. Prior to the concept of negative numbers, negative solutions to problems were considered "false" and equations requiring negative solutions were described as absurd.[3]
Contents |
Introduction
As the result of subtraction
Negative numbers can be thought of as resulting from the subtraction of a larger number from a smaller. For example, negative three is the result of subtracting three from zero:
- 0 − 3 = −3.
In general, the subtraction of a larger number from a smaller yields a negative result, with the magnitude of the result being the difference between the two numbers. For example,
- 5 − 8 = −3
since 8 − 5 = 3.
The number line
The relationship between negative numbers, positive numbers, and zero is often expressed in the form of a number line:
Numbers appearing farther to the right on this line are greater, while numbers appearing farther to the left are less. Thus zero appears in the middle, with the positive numbers to the right and the negative numbers to the left.
Note that a negative number with greater magnitude is considered less. For example even though (positive) 8 is greater than (positive) 5, written
- 8 > 5
negative 8 is considered to be less than negative 5:
- −8 < −5.
In addition, any negative number is less than any positive number, so
- −8 < 5 and −5 < 8.
Signed numbers
In the context of negative numbers, a number that is greater than zero is referred to as positive. Thus every real number other than zero is either positive or negative, while zero itself is not considered to have a sign. Positive numbers are sometimes written with a plus sign in front, e.g. +3 denotes a positive three.
Because zero is neither positive nor negative, the term non-negative is sometimes used to refer to a number that is either positive or zero, while non-positive is used to refer to a number that is either negative or zero.
Arithmetic involving negative numbers
The minus sign "−" signifies the operator for both the binary (two-operand) operation of subtraction (as in y-z) and the unary (one-operand) operation of negation (as in -x, or twice in -(-x)). A special case of unary negation occurs when it operates on a positive number, in which case the result is a negative number (as in -5).
The ambiguity of the "-" symbol does not generally lead to ambiguity in arithmetic expressions, because the order of operations makes only one interpretation or the other possible for each "-". However, it can lead to confusion and be difficult for a person to understand an expression when operator symbols appear adjacent to one another. A solution can be to parenthesize the unary "-" along with its operand.
For example, the expression 7 + −5 may be clearer if written 7 + (−5) (even though they mean exactly the same thing formally). The subtraction expression 7 − 5 is a different expression that doesn't represent the same operations, but it evaluates to the same result.
Sometimes in elementary schools a number may be prefixed by a superscript minus sign or plus sign to explicitly distinguish negative and positive numbers as in[4]
- −2 + −5 gives −7.
Addition
Addition of two negative numbers is very similar to addition of two positive numbers. For example,
- (−3) + (−5) = −8.
The idea is that two debts can be combined into a single debt of greater magnitude.
When adding together a mixture of positive of negative numbers, one can think of the negative numbers as positive quantities as being subtracted. For example:
- 8 + (−3) = 8 − 3 = 5 and (−2) + 7 = 7 − 2 = 5.
In the first example, a credit of 8 is combined with a debt of 3, which yields a total credit of 5. If the negative number has greater magnitude, then the result is negative:
- (−8) + 3 = 3 − 8 = −5 and 2 + (−7) = 2 − 7 = −5.
Here the credit is less than the debt, so the net result is a debt.
Subtraction
As discussed above, it is possible for the subtraction of two non-negative numbers to yield a negative answer:
- 5 − 8 = −3
In general, subtraction of a positive number is the same thing as addition of a negative. Thus
- 5 − 8 = 5 + (−8) = −3
and
- (−3) − 5 = (−3) + (−5) = −8
On the other hand, subtracting a negative number is the same as adding a positive. (The idea is that losing a debt is the same thing as gaining a credit.) Thus
- 3 − (−5) = 3 + 5 = 8
and
- (−5) − (−8) = (−5) + 8 = 3.
Multiplication
When multiplying numbers, the magnitude of the product is always just the product of the two magnitudes. The sign of the product is determined by the following rules:
- The product of one positive number and one negative number is negative.
- The product of two negative numbers is positive.
Thus
- (−2) × 3 = −6
and
- (−2) × (−3) = 6.
The reason behind the first example is simple: adding three −2's together yields −6:
- (−2) × 3 = (−2) + (−2) + (−2) = -6.
The reasoning behind the second example is more complicated. The idea again is that losing a debt is the same thing as gaining a credit. In this case, losing two debts of three each is the same as gaining a credit of six:
- (−2 debts ) × (−3 each) = +6 credit.
The convention that a product of two negative numbers is positive is also necessary for multiplication to follow the distributive law. In this case, we know that
- (−2) × (−3) + 2 × (−3) = (−2 + 2) × (−3) = 0 × (−3) = 0.
Since 2 × (−3) = −6, the product (−2) × (−3) must equal 6.
These rules lead to another (equivalent) rule—the sign of any product a × b depends on the sign of a as follows:
- if a is positive, then the sign of a × b is the same as the sign of b, and
- if a is negative, then the sign of a × b is the opposite of the sign of b.
Division
The sign rules for division are the same as for multiplication. For example,
- 8 ÷ (−2) = −4,
- (−8) ÷ 2 = −4,
and
- (−8) ÷ (−2) = 4.
If dividend and divisor have the same sign, the result is always positive.
Negation
The negative version of a positive number is referred to as its negation. For example, −3 is the negation of the positive number 3. The sum of a number and its negation is equal to zero:
- 3 + −3 = 0.
That is, the negation of a positive number is the additive inverse of the number.
Using algebra, we may write this principle as an algebraic identity:
- x + −x = 0.
This identity holds for any positive number x. It can be made to hold for all real numbers by extending the definition of negation to include zero and negative numbers. Specifically:
- The negation of 0 is 0, and
- The negation of a negative number is the corresponding positive number.
For example, the negation of −3 is +3. In general,
- −(−x) = x.
The absolute value of a number is the non-negative number with the same magnitude. For example, the absolute value of −3 and the absolute value of 3 are both equal to 3, and the absolute value of 0 is 0.
Formal construction of negative integers
In a similar manner to rational numbers, we can extend the natural numbers N to the integers Z by defining integers as an ordered pair of natural numbers (a, b). We can extend addition and multiplication to these pairs with the following rules:
- (a, b) + (c, d) = (a + c, b + d)
- (a, b) × (c, d) = (a × c + b × d, a × d + b × c)
We define an equivalence relation ~ upon these pairs with the following rule:
- (a, b) ~ (c, d) if and only if a + d = b + c.
This equivalence relation is compatible with the addition and multiplication defined above, and we may define Z to be the quotient set N²/~, i.e. we identify two pairs (a, b) and (c, d) if they are equivalent in the above sense. Note that Z, equipped with these operations of addition and multiplication, is a ring, and is in fact, the prototypical example of a ring.
We can also define a total order on Z by writing
- (a, b) ≤ (c, d) if and only if a + d ≤ b + c.
This will lead to an additive zero of the form (a, a), an additive inverse of (a, b) of the form (b, a), a multiplicative unit of the form (a + 1, a), and a definition of subtraction
- (a, b) − (c, d) = (a + d, b + c).
This construction is a special case of the Grothendieck construction.
Uniqueness
The negative of a number is unique, as is shown by the following proof.
Let x be a number and let y be its negative. Suppose y′ is another negative of x. By an axiom of the real number system
And so, x + y′ = x + y. Using the law of cancellation for addition, it is seen that y′ = y. Thus y is equal to any other negative of x. That is, y is the unique negative of x.
History
Negative numbers appear for the first time in history in the Nine Chapters on the Mathematical Art (Jiu zhang suan-shu), which in its present form dates from the period of the Han Dynasty (202 BC. – AD 220), but may well contain much older material.[2] The Nine Chapters used red counting rods to denote positive coefficients and black rods for negative.[5] (This system is the exact opposite of contemporary printing of positive and negative numbers in the fields of banking, accounting, and commerce, wherein red numbers denote negative values and black numbers signify positive values). The Chinese were also able to solve simultaneous equations involving negative numbers.
For a long time, negative solutions to problems were considered "false". In Hellenistic Egypt, Diophantus in the third century A.D. referred to an equation that was equivalent to 4x + 20 = 0 (which has a negative solution) in Arithmetica, saying that the equation was absurd.
The use of negative numbers was known in early India, and their role in situations like mathematical problems of debt was understood.[6] Consistent and correct rules for working with these numbers were formulated.[7] The diffusion of this concept led the Arab intermediaries to pass it to Europe.[6]
The ancient Indian Bakhshali Manuscript, which Pearce Ian claimed was written some time between 200 BC. and AD 300,[8] while George Gheverghese Joseph dates it to about AD 400 and no later than the early 7th century,[9] carried out calculations with negative numbers, using "+" as a negative sign.[10]
During the 7th century AD, negative numbers were used in India to represent debts. The Indian mathematician Brahmagupta, in Brahma-Sphuta-Siddhanta (written in A.D. 628), discussed the use of negative numbers to produce the general form quadratic formula that remains in use today. He also found negative solutions of quadratic equations and gave rules regarding operations involving negative numbers and zero, such as "A debt cut off from nothingness becomes a credit; a credit cut off from nothingness becomes a debt. " He called positive numbers "fortunes," zero "a cipher," and negative numbers "debts."[11][12]
During the 8th century AD, the Islamic world learned about negative numbers from Arabic translations of Brahmagupta's works, and by the 10th century Islamic mathematicians were using negative numbers for debts. The earliest known Islamic text that uses negative numbers is A Book on What Is Necessary from the Science of Arithmetic for Scribes and Businessmen by Abū al-Wafā' al-Būzjānī.[13]
In the 12th century AD in India, Bhāskara II also gave negative roots for quadratic equations but rejected them because they were inappropriate in the context of the problem. He stated that a negative value is "in this case not to be taken, for it is inadequate; people do not approve of negative roots."
Knowledge of negative numbers eventually reached Europe through Latin translations of Arabic and Indian works.
European mathematicians, for the most part, resisted the concept of negative numbers until the 17th century, although Fibonacci allowed negative solutions in financial problems where they could be interpreted as debits (chapter 13 of Liber Abaci, AD 1202) and later as losses (in Flos).
In the 15th century, Nicolas Chuquet, a Frenchman, used negative numbers as exponents and referred to them as “absurd numbers.”
In A.D. 1759, Francis Maseres, an English mathematician, wrote that negative numbers "darken the very whole doctrines of the equations and make dark of the things which are in their nature excessively obvious and simple". He came to the conclusion that negative numbers were nonsensical.[14]
In the 18th century it was common practice to ignore any negative results derived from equations, on the assumption that they were meaningless.[15]
See also
Notes
- ^ Different languages have different conventions regarding the sign of zero. For example, in French, zero is considered to be both positive and negative. The French words positif and négatif mean the same as English "positive or zero" and "negative or zero" respectively.
- ^ a b Struik, page 32–33. "In these matrices we find negative numbers, which appear here for the first time in history."
- ^ Diophantus, Arithmetica.
- ^ Grant P. Wiggins; Jay McTighe (2005). Understanding by design. ACSD Publications. p. 210. ISBN 1416600353.
- ^ Temple, Robert. (1986). The Genius of China: 3,000 Years of Science, Discovery, and Invention. With a forward by Joseph Needham. New York: Simon & Schuster, Inc. ISBN 0671620282. Page 141.
- ^ a b Bourbaki, page 49
- ^ Britannica Concise Encyclopedia (2007). algebra
- ^ Pearce, Ian (May 2002). "The Bakhshali manuscript". The MacTutor History of Mathematics archive. http://www-history.mcs.st-andrews.ac.uk/HistTopics/Bakhshali_manuscript.html. Retrieved 2007-07-24.
- ^ Teresi, Dick. (2002). Lost Discoveries: The Ancient Roots of Modern Science–from the Babylonians to the Mayas. New York: Simon & Schuster. ISBN 0684837188. Page 65–66.
- ^ Teresi, Dick. (2002). Lost Discoveries: The Ancient Roots of Modern Science–from the Babylonians to the Mayas. New York: Simon & Schuster. ISBN 0684837188. Page 65.
- ^ Colva M. Roney-Dougal, Lecturer in Pure Mathematics at the University of St Andrews, stated this on the BBC Radio 4 programme "In Our Time," on 9 March 2006.
- ^ Knowledge Transfer and Perceptions of the Passage of Time, ICEE-2002 Keynote Address by Colin Adamson-Macedo. "Referring again to Brahmagupta's great work, all the necessary rules for algebra, including the 'rule of signs', were stipulated, but in a form which used the language and imagery of commerce and the market place. Thus 'dhana' (= fortunes) is used to represent positive numbers, whereas 'rina' (= debts) were negative".
- ^ Hashemipour, Behnaz (2007). "Būzjānī: Abū al‐Wafāʾ Muḥammad ibn Muḥammad ibn Yaḥyā al‐Būzjānī". In Thomas Hockey et al. The Biographical Encyclopedia of Astronomers. New York: Springer. pp. 188–9. ISBN 9780387310220. http://islamsci.mcgill.ca/RASI/BEA/Buzjani_BEA.htm. (PDF version)
- ^ Maseres, Francis (1758). A dissertation on the use of the negative sign in algebra: containing a demonstration of the rules usually given concerning it; and shewing how quadratic and cubic equations may be explained, without the consideration of negative roots. To which is added, as an appendix, Mr. Machin's Quadrature of the Circle.
- ^ Martinez, Alberto A. (2006). Negative Math: How Mathematical Rules Can Be Positively Bent. Princeton University Press. a history of controversies on negative numbers, mainly from the 1600s until the early 1900s.
References
- Bourbaki, Nicolas (1998). Elements of the History of Mathematics. Berlin, Heidelberg, and New York: Springer-Verlag. ISBN 3540647678.
- Struik, Dirk J. (1987). A Concise History of Mathematics. New York: Dover Publications.
External links
- Maseres' biographical information
- BBC Radio 4 series "In Our Time," on Negative Numbers, March 9, 2006
- Endless Examples & Exercises: Operations with Signed Integers
- Math Forum: Ask Dr. Math FAQ: Negative Times a Negative
|
|||||||||||
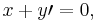
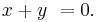
 )
) )
) )
) )
) )
) )
) )
) )
) )
)